Tag Archives: path

Computer Algorithms: Dijkstra Shortest Path in a Graph

algorithms, data structures, Graphs, , , , , , , , , , , , , , , , , ,

Introduction

We already know how we can find the shortest paths in a graph starting from a given vertex. Practically we modified breadth-first search in order to calculate the distances from s to all other nodes reachable from s. We know that this works because BFS walks through the graph level by level.

BFS Shortest Paths
BFS is often used to find shortest paths between a starting node (s) and all other reachable nodes in a graph!

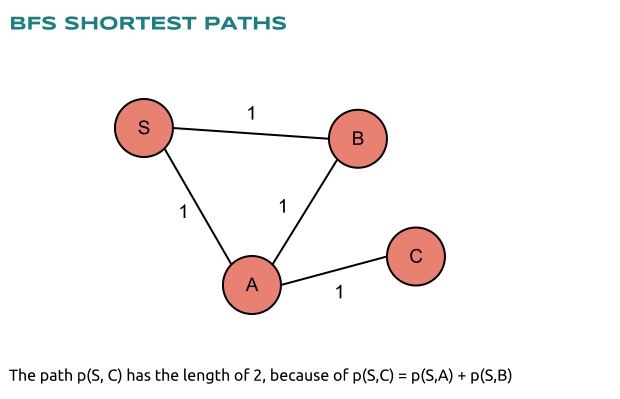
Some sources give a very simple explanation of how BFS finds the shortest paths in a graph. We must just think of the graph as a set of balls connected through strings.

The Graph as Balls and Strings
We can think of a graph as a set of balls connected through strings!

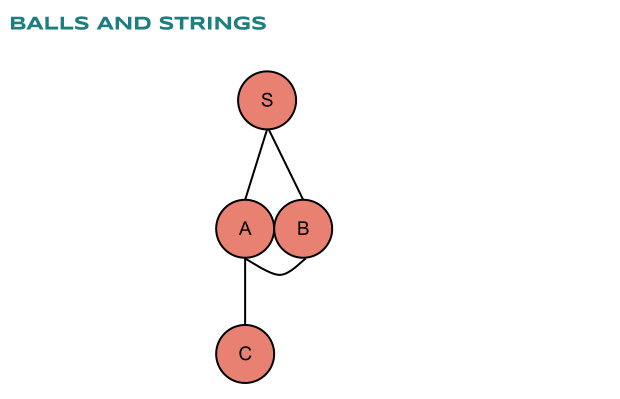
As we can see by lifting the ball called “S” all other balls fall down. The closest balls are directly connected to “s” and this is the first level, while the outermost balls are those with longest paths.

The Graph as Balls and Strings Levels
Breadth-first search works much like the image above – it explores the graph level by level, thus we’re sure that all the paths are the shortest!

Clearly edges like those between A and B doesn’t matter for our BFS algorithm because they don’t make the path from S to C through B shorter. This is also known as the triangle inequality, where the sum of the lengths of two of the sides of the triangle is always greater than the length of the third side.

Triangle inequality
What the triangle inequality says us is that if we have a direct edge between two nodes – that must be the shortest path between them!

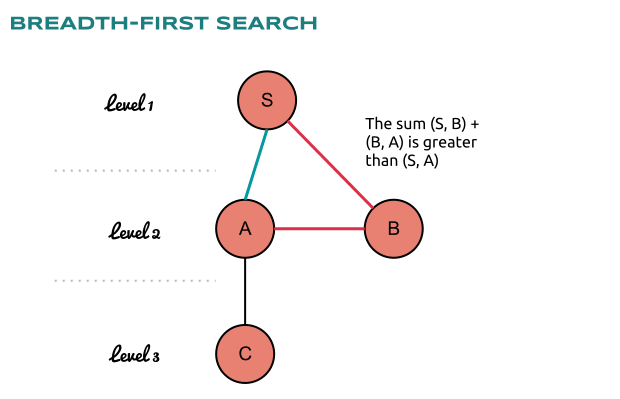
We must only answer the question is BFS the best algorithm that finds the shortest path between any two nodes of the graph? This is a reasonable question because as we know by using BFS we don’t find only the shortest path between given vertices i and j, but we also get the shortest paths between i and all other vertices of G. This is an information that we actually don’t need, but can we find the shortest path between i and j without that info? Continue reading Computer Algorithms: Dijkstra Shortest Path in a Graph →

Computer Algorithms: Shortest Path in a Graph

algorithms, data structures, Graphs, , , , , , , , , , , , , , , , , , , ,

Introduction

Since with graphs we can represent real-life problems it’s almost clear why we would need an efficient algorithm that calculates the shortest path between two vertices. Getting back to our example of a road map we can use such an algorithm in order to find the shortest path between two cities. This example, of course, is very basic indeed, but it can give us a clear example of where shortest path can be applied.

In the other hand, we can model an enormous field of real-life problems using graphs – not only road maps. As we already know, whenever we have relations between different abstract objects we can refer an efficient graph algorithm.

OK, so we need a shortest path algorithm, but before we proceed with the exact algorithm first we’ll need to answer some questions and give some definitions.

Overview

First we need a definition of the terms distance and path between two nodes. A path is considered to be the sequence of vertices (or edges if you wish) between two vertices i and j. Of course we assume that there might be no path between any to vertices in the graph! Also we assume that this definition relates both for directed and undirected graphs. After we have the definition of a path we can proceed by defining a “distance”, which is said to be the number of edges in the path between i and j.

Path and Distance
First we need to define what’s a path and a distance between two vertices in order to continue searching for the shortest path!
Continue reading Computer Algorithms: Shortest Path in a Graph →

PHP Strings: How to Get the Extension of a File

micro tutorial, PHP, , , , , , , , ,

EXE or GIF or DLL or …

Most of the code chunks I’ve seen about getting a file extension from a string are based on some sort of string manipulation.

Get the Filename Extension with PHP
If you want to get the filename extension with PHP is better to use pathinfo() than string manipulations

$filename = '/my/path/image.jpeg';
echo substr($filename, strrpos($filename, '.') + 1);

Howerver there is a more elegant solution.

$filename = '/my/path/image.jpeg';
echo strtolower(pathinfo($filename, PATHINFO_EXTENSION));

Thus you rely on PHP built in functions and it’s harder to overlook the exact string manipulation approach.

jQuery: Setting Up a Vector Path Fill Color

micro tutorial, , , , , , , , , , ,

It’s quite unusual to think of the jQuery’s attr() method as a generic method that can only change basic attributes as value, style, etc. However attr() can change whatever DOM element attribute. In this case you may know that the SVG path element can have a fill attribute, so you can simply setup a:

$('path').attr('fill', '#ccc');