Tag Archives: Environment

Computer Algorithms: Prim’s Minimum Spanning Tree

algorithms, data structures, Graphs, , , , , , , , , , , , , , , ,

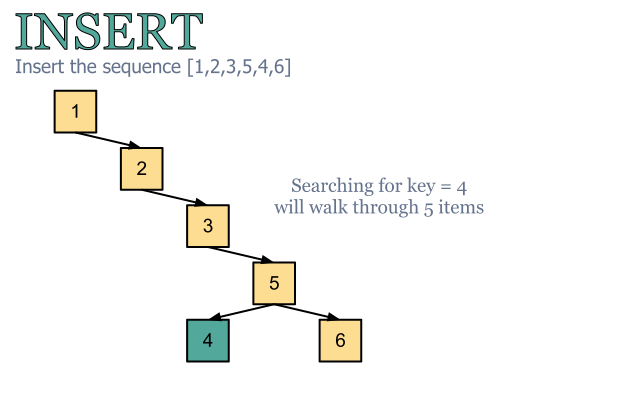
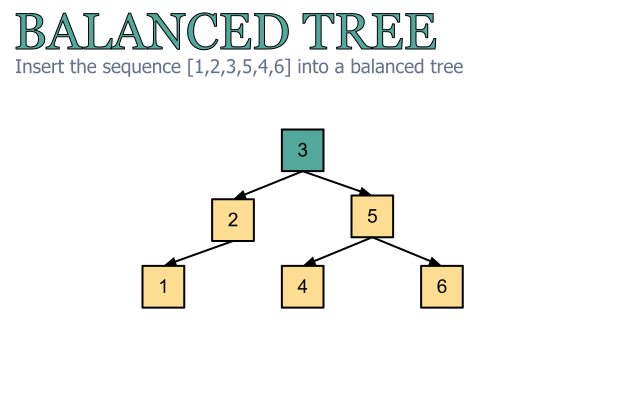
Introduction

Along with the Kruskal’s minimum spanning tree algorithm, there’s another general algorithm that solves the problem. The algorithm of Prim.

As we already know the algorithm of Kruskal works in a pretty natural and logical way. Since we’re trying to build a MST, which is naturally build by the minimal edges of the graph (G), we sort them in a non-descending order and we start building the tree.

The algorithm of Kruskal
 

During the whole process of building the final minimum spanning tree Kruskal’s algorithm keeps a forest of trees. The number of trees in that forest decreases on each step and finally we get the minimum weight spanning tree.

A key point in the Kruskal’s approach is the way we get the “next” edge from G that should be added to one of the trees of the forest (or to connect two trees from the forest). The only thing we should be aware of is to choose an edge that’s connecting two vertices – u and v and these two shouldn’t be in the same tree. That’s all.

The Kruskal's Tricky Part
 

An important feature of the Kruskal’s algorithm is that it builds the MST just by sorting the edges by their weight and doesn’t care about a particular starting vertex.

In the same time there’s another algorithm that builds a MST – the algorithm of Prim designed by Robert Prim in 1957. Continue reading Computer Algorithms: Prim’s Minimum Spanning Tree →

Computer Algorithms: Kruskal’s Minimum Spanning Tree

algorithms, data structures, Graphs, , , , , , , , , , , , , , , , ,

Introduction

One of the two main algorithms in finding the minimum spanning tree algorithms is the algorithm of Kruskal. Before getting into the details, let’s get back to the principles of the minimum spanning tree.

We have a weighted graph and of all spanning trees we’d like to find the one with minimal weight. As an example on the picture above you see a spanning tree (T) on the graph (G), but that isn’t the minimum weight spanning tree!

A graph and a possible spanning tree
 
Continue reading Computer Algorithms: Kruskal’s Minimum Spanning Tree →

Computer Algorithms: Balancing a Binary Search Tree

algorithms, data structures, , , , , , , , , , , , , , , , , , , ,

Introduction

The binary search tree is a very useful data structure, where searching can be significantly faster than searching into a linked list. However in some cases searching into a binary tree can be as slow as searching into a linked list and this mainly depends on the input sequence. Indeed in case the input is sorted the binary tree will seem much like a linked list and the search will be slow.

Inserting into a binary search tree
A binary search tree may seem much like a linked lists if the input is nearly sorted!

To overcome this we must change a bit the data structure in order to stay well balanced. It’s intuitively clear that the searching process will be better if the tree is well branched. This is when finding an item will become faster with minimal effort.

Balanced tree
Searching into a balanced tree is significantly faster than searching into a non-balanced tree!

Since we know how to construct a binary search tree the only thing left is to keep it balanced. Obviously we will need to re-balance the tree on each insert and delete, which will make this data structure more difficult to maintain compared to non-balanced search trees, but searching into it will be significantly faster. Continue reading Computer Algorithms: Balancing a Binary Search Tree →

Computer Algorithms: Binary Search Tree

algorithms, data structures, , , , , , , , , , , , , , , , , , , ,

Introduction

Constructing a linked list is a fairly simple task. Linked lists are a linear structure and the items are located one after another, each pointing to its predecessor and its successor. Almost every operation is easy to code in few lines and doesn’t require advanced skills. Operations like insert, delete, etc. over linked lists are performed in a linear time. Of course on small data sets this works fine, but as the data grows these operations, especially the search operation becomes too slow.

Indeed searching in a linked list has a linear complexity and in the worst case we must go through the entire list in order to find the desired element. The worst case is when the item doesn’t belong to the list and we must check every single item of the list even the last one without success. This approach seems much like the sequential search over arrays. Of course this is bad when we talk about large data sets.

Search over Linked Lists and Arrays
Sequential search over arrays seems much like searching in linked lists and it is a basically ineffective opration!
Continue reading Computer Algorithms: Binary Search Tree →

Google Closure Compiler doesn’t work?!

web development, , , , , , , , , , , , ,

What are these strange java errors?

No, it works but maybe the problem is you current Java version. The Google Closure Compiler requires 1.6 and most commonly you’re runing on 1.5 therefore it produces errors. It was my problem when I tried to run the application. At that moment it produced these lines of errors:

java -jar compiler.jar --help

Exception in thread “main” java.lang.UnsupportedClassVersionError: Bad version number in .class file
at java.lang.ClassLoader.defineClass1(Native Method)
at java.lang.ClassLoader.defineClass(ClassLoader.java:676)
at java.security.SecureClassLoader.defineClass(SecureClassLoader.java:124)
at java.net.URLClassLoader.defineClass(URLClassLoader.java:260)
at java.net.URLClassLoader.access$100(URLClassLoader.java:56)
at java.net.URLClassLoader$1.run(URLClassLoader.java:195)
at java.security.AccessController.doPrivileged(Native Method)
at java.net.URLClassLoader.findClass(URLClassLoader.java:188)
at java.lang.ClassLoader.loadClass(ClassLoader.java:317)
at sun.misc.Launcher$AppClassLoader.loadClass(Launcher.java:280)
at java.lang.ClassLoader.loadClass(ClassLoader.java:252)
at java.lang.ClassLoader.loadClassInternal(ClassLoader.java:375)

Just update or switch your current Java version to 1.6 and everything will be fine!