stoimen's web log

Introduction

One of the two main algorithms in finding the minimum spanning tree algorithms is the algorithm of Kruskal. Before getting into the details, let’s get back to the principles of the minimum spanning tree.

We have a weighted graph and of all spanning trees we’d like to find the one with minimal weight. As an example on the picture above you see a spanning tree (T) on the graph (G), but that isn’t the minimum weight spanning tree!

We can think of a group of islands and the possible connections of bridges connecting them. Of course building bridges is expensive and time consuming, so we must be aware of what kind of bridges we want to build. Nevertheless there is an important question, what’s the minimum price we’d like to pay to build such set of bridges connecting all the islands.

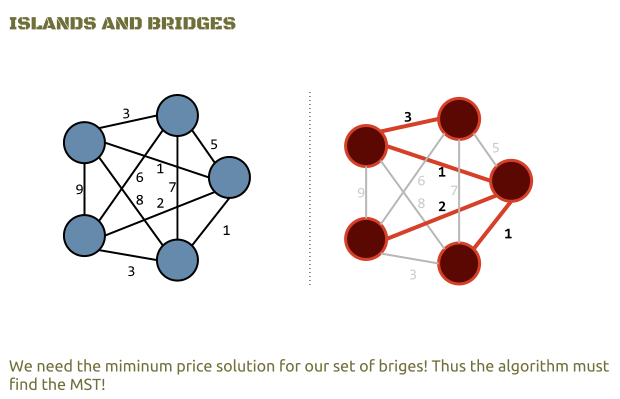
Thus we practically need to build a minimum spanning tree, where the vertices will be the islands, while the edges will be the possible bridges between them. Every possible bridge has a weight (the price or the time we need to build it, etc.).

This scenario is only one of possible use cases of where minimum spanning trees can be used in practice.

The two main approaches – the Kruskal’s and the Prim’s algorithms however differ.

Overview

The algorithm of Kruskal starts by initializing a set of |V| trees.

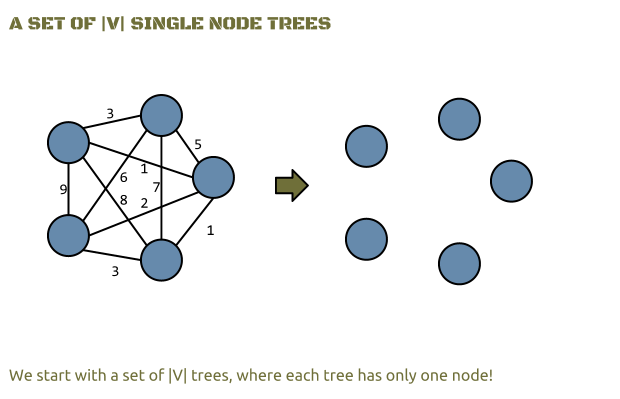
During the process of building the final spanning tree we keep a forest. Obviously we start with a forest with |V| trees, where each tree is a single node tree.

On some point we have a forest of “k” trees which are all a sub-trees of the minimum spanning tree.

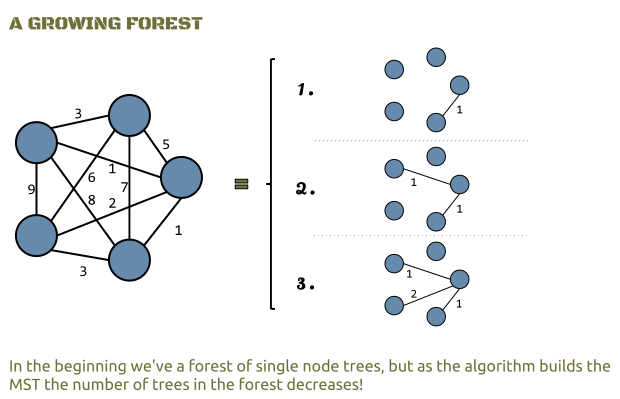
Finally one step before building the final MST we have two trees and we connect them with the less weighted edge left that connects them.

It’s important to note that during the process of building the tree we sort the edges in ascending order by their weight.

Than we start getting edges and check whether their ends (the two vertices making the edge) belong to a different sub-trees.

Pseudo Code

1. T (the final spanning tree) is defined to be the empty set;
2. For each vertex v of G, make the empty set out of v;
3. Sort the edges of G in ascending (non-decreasing) order;
4. For each edge (u, v) from the sored list of step 3.
      If u and v belong to different sets
         Add (u,v) to T;
         Get together u and v in one single set;
5. Return T

A great feature about the Kruskal’s algorithm is that it also work on disconnected graphs.

History

Kruskal’s algorithm is named after Joseph Kruskal, who wasn’t only computer scientist, but also prominent mathematician and statistician. Although he is best known for its algorithm for computing the minimum spanning tree, described in this post, he’s also known with his work as a statistician and his contribution to the formulation of multidimensional scaling.

Kruskal also explored the Indo-European languages contributing the studies of the linguistics along with other scientists. His “Indo-European Lexicographical List” (http://www.wordgumbo.com/ie/cmp/) is still widely used.

9 thoughts on “Computer Algorithms: Kruskal’s Minimum Spanning Tree”

For the curious readers, here’s the PHP implementation of Kruskal’s algorithm.

// the graph
$G = array(
    0 => array( 0,  4,  0,  0,  0,  0,  0,  0,  8),
    1 => array( 4,  0,  8,  0,  0,  0,  0,  0,  11),
    2 => array( 0,  8,  0,  7,  0,  4,  2,  0,  0),
    3 => array( 0,  0,  7,  0,  9,  14,  0,  0,  0),
    4 => array( 0,  0,  0,  9,  0,  10,  0,  0,  0),
    5 => array( 0,  0,  4,  14,  10,  0,  0,  2,  0),
    6 => array( 0,  0,  2,  0,  0,  0,  0,  6,  7),
    7 => array( 0,  0,  0,  0,  0,  2,  6,  0,  1),
    8 => array( 8,  11,  0,  0,  0,  0,  7,  1,  0),
);
 
function Kruskal(&$G)
{
    $len = count($G);
 
    // 1. Make T the empty tree (we'll modify the array G to keep only MST
    $T = array();
 
    // 2. Make a single node trees (sets) out of each vertex
    $S = array();
    foreach (array_keys($G) as $k) {
        $S[$k] = array($k);
    }
 
    // 3. Sort the edges
    $weights = array();
    for ($i = 0; $i < $len; $i++) {
        for ($j = 0; $j < $i; $j++) {
            if (!$G[$i][$j]) continue;
 
            $weights[$i . ' ' . $j] = $G[$i][$j];
        }
    }
    asort($weights);
 
    foreach ($weights as $k => $w) {
        list($i, $j) = explode(' ', $k);
 
        $iSet = find_set($S, $i);
        $jSet = find_set($S, $j);
        if ($iSet != $jSet) {
            $T[] = "Edge: ($i, $j)";
            union_sets($S, $iSet, $jSet);
        }
    }
 
    return $T;
}
 
function find_set(&$set, $index)
{
    foreach ($set as $k => $v) {
        if (in_array($index, $v)) {
            return $k;
        }
    }
 
    return false;
}
 
function union_sets(&$set, $i, $j)
{
    $a = $set[$i];
    $b = $set[$j];
    unset($set[$i], $set[$j]);
    $set[] = array_merge($a, $b);
}
 
$mst = Kruskal($G);
 
//Edge: (8, 7)
//Edge: (6, 2)
//Edge: (7, 5)
//Edge: (1, 0)
//Edge: (5, 2)
//Edge: (3, 2)
//Edge: (2, 1)
//Edge: (4, 3)
foreach ($mst as $v) {
    echo $v . PHP_EOL;
}

Hi, indeed a great work here in the first place. Keep going!

In step 2, you are saying to make empty set out of each vertex of G. In my opinion, it shall be 1-element set containing exactly the given vertex. After in the loop, if the vertices are in different components, the sets containing u and v are joined.

I’m triying to program this algorithm with C++
I need to keep the size of the distance matrix variable…
Any suggestions?
Thanks

Hi!
Is it possible to let the user chose the graphe by puting the value in the form?
and How can we do it ?And how can we store the graph that we have to use to find the tree whith kruskal algorithm?

Good morning ,

Could anyone solve this question ??
or explain it for me !!

(Kruskal)
Give an example of a family of graphs with n nodes and O(n) edges such that a naive implementation
of the union-find data structure without union-by-rank and path compression
leads to quadratic running time for Kruskal’s algorithm.

would this work with a loop-tree, one where an edge is added between exactly one of the leaves and another node in the tree?

I am not able to understand the pseudocode.Please help me.

Just managed to implement it after almost four years. Took some time, but I managed to do it in O(N^2).

I don’t want implementation,just give me an algorithm.

stoimen's web log

on web development

Computer Algorithms: Kruskal’s Minimum Spanning Tree

Introduction

Overview

Pseudo Code

History

9 thoughts on “Computer Algorithms: Kruskal’s Minimum Spanning Tree”

Leave a Reply Cancel reply