Introduction
When it comes to sorting items by comparing them merge sort is one very natural approach. It is natural, because simply divides the list into two equal sub-lists then sort these two partitions applying the same rule. That is a typical divide and conquer algorithm and it just follows the intuitive approach of speeding up the sorting process by reducing the number of comparisons. However there are other “divide and conquer” sorting algorithms that do not follow the merge sort scheme, while they have practically the same success. Such an algorithm is quicksort.
Overview
Back in 1960 C. A. R. Hoare comes with a brilliant sorting algorithm. In general quicksort consists of some very simple steps. First we’ve to choose an element from the list (called a pivot) then we must put all the elements with value less than the pivot on the left side of the pivot and all the items with value greater than the pivot on its right side. After that we must repeat these steps for the left and the right sub-lists. That is quicksort! Simple and elegant!
It is a pure divide and conquer approach as merge sort, but while merge sort’s tricky part was merging the sorted sub-lists, in quicksort there are other things to consider.
First of all obviously the choice of a pivot is the bottleneck. Indeed it all depends on that pivot. Imagine that you choose the greatest value from the list – than you’ve to put all the other items of the list into the “left” sub-list. If you do that on each step you’ll practically go into the worst scenario and that is no good. The thing is that in the worst case quicksort is not so effective and it’s practically as slow as bubble sort and insertion sort. The good thing is that in practice with randomly generated lists there is not a high possibility to go into the worst case of quicksort.
Choosing a pivot
Of course the best pivot is the middle element from the list. Thus the list will be divided into two fairly equal sub-lists. The problem is that there’s not an easy way to get the middle element from a list and this will slow down the algorithm. So typically we can get for a pivot the first or the last item of the list.
After choosing a pivot the rest is simple. Put every item with a greater value on the right and every item with a lesser value on the left. Then we must sort the left and right sub-lists just as we did with the initial list.
It’s clear that with this algorithm naturally we’re going into a recursive solution. Typically every divide and conquer approach is easy to implement with recursion. But because recursion can be heavy, there is an iterative approach.
Implementation
As I said above recursive approach is something very natural for quicksort as it follows the divide and conquer principles. On each step we divide the list in two and we pass those sub-lists to our recursive function. But recursion is dangerous sometimes, so an iterative approach is also available. Typically iterative approaches “model” recursion with extra memory and a model of a stack, which is our case. Here we have two examples of quicksort – recursive and iterative in PHP. Let’s go first with the recursion.
Recursive Quicksort
$list = array(5,3,9,8,7,2,4,1,6,5); // recursive function quicksort($array) { if (count($array) == 0) { return array(); } $pivot = $array[0]; $left = $right = array(); for ($i = 1; $i < count($array); $i++) { if ($array[$i] < $pivot) { $left[] = $array[$i]; } else { $right[] = $array[$i]; } } return array_merge(quicksort($left), array($pivot), quicksort($right)); } // 1, 2, 3, 4, 5, 5, 6, 7, 8, 9 print_r(quicksort($list)); |
Iterative Quicksort
$list = array(5,3,9,8,7,2,4,1,6,5); // iterative function quicksort_iterative($array) { $stack = array($array); $sorted = array(); while (count($stack) > 0) { $temp = array_pop($stack); if (count($temp) == 1) { $sorted[] = $temp[0]; continue; } $pivot = $temp[0]; $left = $right = array(); for ($i = 1; $i < count($temp); $i++) { if ($pivot > $temp[$i]) { $left[] = $temp[$i]; } else { $right[] = $temp[$i]; } } $left[] = $pivot; if (count($right)) array_push($stack, $right); if (count($left)) array_push($stack, $left); } return $sorted; } // 1, 2, 3, 4, 5, 5, 6, 7, 8, 9 print_r(quicksort_iterative($list)); |
Complexity
The complexity of quicksort in the average case is O(n*log(n)) – same as Merge sort. The problem is that in the worst case it is O(n2) – same as bubble sort. Obviously the worst case is when we have an already sorted list, and we constantly take for a pivot the last element of the list. But we should consider that in practice we don’t quite use sorted lists that we have to sort again, right?
Application
Quicksort is a great sorting algorithm and developers often go for it, but let’s see some pros and cons of it.
Why using quicksort
- Recursive implementation is easy
- In general its speed is same as merge sort – O(n*log(n))
- Elegant solution with no tricky merging as merge sort
Why not using quicksort
- As slow as bubble sort in the worst case!
- Iterative implementation isn’t easy
- There are faster algorithms for some sets of data types
Quicksort is beautiful because of the elegant idea behind its principles. Indeed if you have two sorted lists one with items with a greater value from a given value and the other with items smaller form that given value you can simply concatenate them and you can be sure that the resulting list will be sorted with no need of special merge.
In fact quicksort is a very elegant general purpose sorting algorithm and every developer should be familiar with its principles.
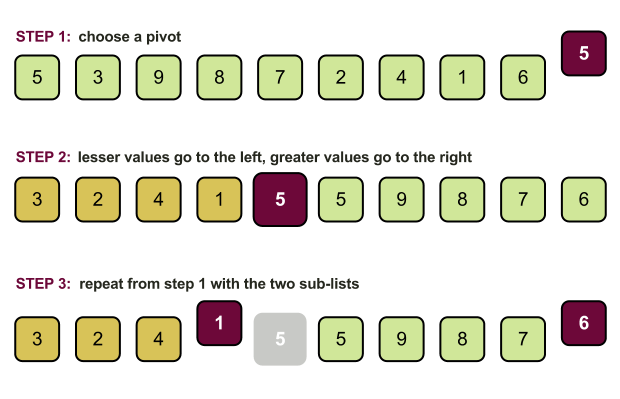


I have recently read a brillinat article: Optimized QuickSort http://alienryderflex.com/quicksort/
There is only the iteretive version, but the recursive one can be very easy implemented based on that.
It completely eliminates the need for two more arrays “left” and “right” each time the function calls itself and I belive it is much faster than any other implementation.
Here is my recursive implementation, with no swaps between the elements of the array and the random-choosed pivot( only at the beginning ):
template
inline void quickSort( T* sort, const unsigned size )
{
quickSortHelp( sort, 0, size – 1 );
}
template
void quickSortHelp( T* sort, const unsigned begin, const unsigned end )
{
if ( begin < end )
{
register unsigned L = begin;
register unsigned R = end;
unsigned index = rand() % ( end – begin + 1 ) + begin;
register T pivot = sort[ index ];
swappy( sort[ index ], sort[ end ] );
while ( L < R )
{
while ( sort[ L ] < pivot && L < R )
L++;
if ( L pivot && L < R )
R–;
if ( L < R )
sort[ L++ ] = sort[ R ];
}
sort[ L ] = pivot;
if ( R < 1 )
R++;
quickSortHelp( sort, begin, R – 1 );
quickSortHelp( sort, L + 1, end );
}
}