Introduction

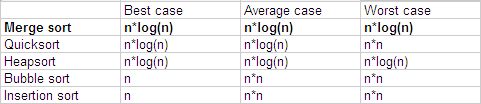
Basically sorting algorithms can be divided into two main groups. Such based on comparisons and such that are not. I already posted about some of the algorithms of the first group. Insertion sort, bubble sort and Shell sort are based on the comparison model. The problem with these three algorithms is that their complexity is O(n²) so they are very slow.

So is it possible to sort a list of items by comparing their items faster than O(n²)? The answer is yes and here’s how we can do it.

The nature of those three algorithms mentioned above is that we almost compared each two items from initial list.

This, of course, is not the best approach and we don’t need to do that. Instead we can try to divide the list into smaller lists and then sort them. After sorting the smaller lists, which is supposed to be easier than sorting the entire initial list, we can try to merge the result into one sorted list. This technique is typically known as “divide and conquer”.

Normally if a problem is too difficult to solve, we can try to break it apart into smaller sub-sets of this problem and try to solve them. Then somehow we can merge the results of the solved problems.

Overview

Merge sort is a comparison model sorting algorithm based on the “divide and conquer” principle. So far so good, so let’s say we have a very large list of data, which we want to sort. Obviously it will be better if we divide the list into two sub-lists with equal length and then sort them. If they remain too large, we can continue breaking them down until we get to something very easy to sort as shown on the diagram bellow.

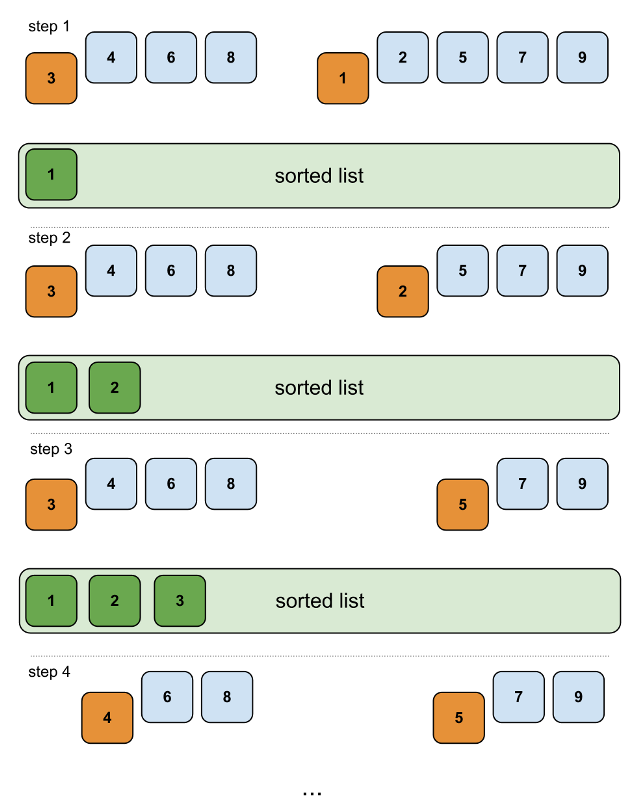
The thing is that on some step of the algorithm we have two sorted lists and the tricky part is to merge them. However this is not so difficult.
We can start comparing the first items of the lists and than we can pop the smaller of them both and put it into a new list containing the merged (sorted) array.

Implementation

The good news is that this algorithm is fast, but not so difficult to implement and that sounds quite good from a developer’s point of view. Here’s the implementation in PHP. Note that every algorithm that follows the divide and conquer principles can be easily implemented in a recursive solution. However recursion can be bitter so you can go for a iterative solution. Typically recursion is “replaced” by additional memory space in iterative solutions. Here’s a recursive version of merge sort.

$input = array(6, 5, 3, 1, 8, 7, 2, 4);
 
function merge_sort($arr)  
{  
	if (count($arr) <= 1) {
		return $arr;  
	}
 
	$left = array_slice($arr, 0, (int)(count($arr)/2));  
	$right = array_slice($arr, (int)(count($arr)/2));  
 
	$left = merge_sort($left);  
	$right = merge_sort($right);  
 
	$output = merge($left, $right);  
 
	return $output;  
}  
 
 
function merge($left, $right)  
{  
	$result = array();  
 
	while (count($left) > 0 && count($right) > 0) {  
		if ($left[0] <= $right[0]) {  
			array_push($result, array_shift($left));  
		} else {  
			array_push($result, array_shift($right));  
		}  
	}  
 
	array_splice($result, count($result), 0, $left);  
	array_splice($result, count($result), 0, $right);  
 
	return $result;  
}  
 
// 1, 2, 3, 4, 5, 6, 7, 8
$output = merge_sort($input);

Complexity

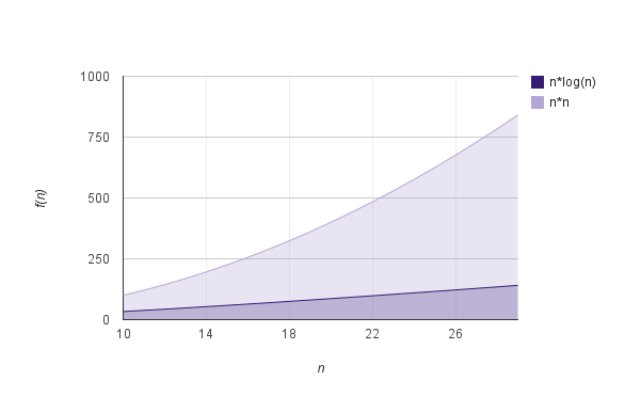
It’s great that the complexity of merge sort is O(n*log(n)) even in the worst case! Note that even quicksort’s complexity can be O(n²) in the worst case. So we can be sure that merge sort is very stable no matter the input.

Two reasons why merge sort is useful

1. Fast no matter the input

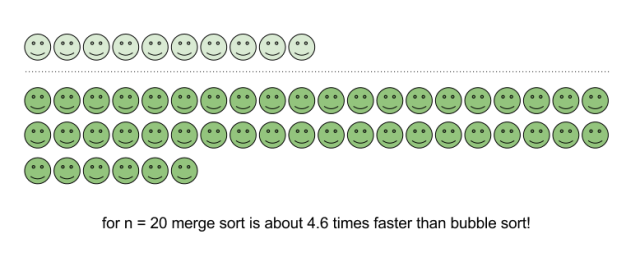
Merge sort is a great sorting algorithm mainly because it’s very fast and stable. It’s complexity is the same even in the worst case and it is O(n*log(n)). Note that even quicksort’s complexity is O(n²) in the worst case, which for n = 20 is about 4.6 times slower!

2. Easy implementation

Another cool reason is that merge sort is easy to implement. Indeed most of the developer consider something fast to be difficult to implement, but that’s not the case of merge sort.

Three reasons why merge sort is not useful

1. Slower than non-comparison based algorithms

Merge sort is however based on the comparison model and as such can be slower than algorithms non-based on comparisons that can sort data in linear time. Of course, this depends on the input data, so we must be careful for the input.

2. Difficult to implement for beginners

Although I don’t think this can be the main reason why not to use merge sort some people say that it can be difficult to implement for beginners, especially the merge part of the algorithm.

3. Slower than insertion and bubble sort for nearly sorted input

Again it is very important to know the input data. Indeed if the input is nearly sorted the insertion sort or bubble sort can be faster. Note that in the best case insertion and bubble sort complexity is O(n), while merge sort’s best case is O(n*log(n)).

As a conclusion I can say that merge sort is practically one of the best sorting algorithms because it’s easy to implement and fast, so it must be considered by every developer!