Introduction
We already know what’s topological sort of a directed acyclic graph. So why do we need a revision of this algorithm? First of all I never mentioned its complexity, thus to understand why we do need a revision let’s get again on the algorithm.
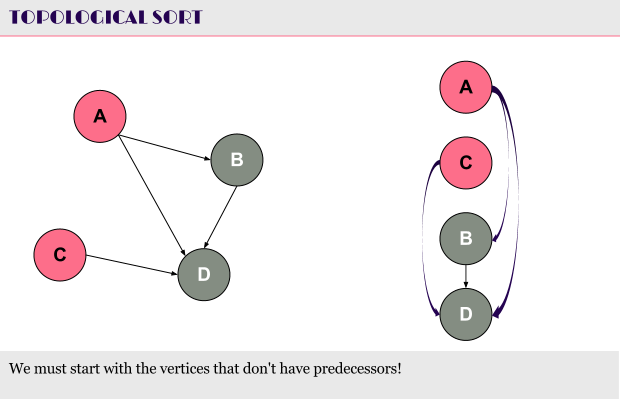
We have a directed acyclic graph (DAG). There are no cycles so we must go for some kind of order putting all the vertices of the graph in such an order, that if there’s a directed edge (u, v), u must precede v in that order.

The process of putting all the vertices of the DAG in such an order is called topological sorting. It’s commonly used in task scheduling or while finding the shortest paths in a DAG.
The algorithm itself is pretty simple to understand and code. We must start from the vertex (vertices) that don’t have predecessors.