Introduction

Let’s assume we have a list of tasks to accomplish. Some of the tasks depend on others, so we must be very careful with the order of their execution. If the relationship between these tasks were simple enough we could represent them as a linked list, which would be great, and we would know the exact order of their execution. The problem is that sometimes the relations between the different tasks are more complex and some tasks depend on two or more other tasks, which in their turn depend on one or more tasks, etc.

Thus we can’t model this problem using linked lists or trees. The only rational solution is to model the problem using a graph. What kind of graph do we need? Well, we definitely need a directed graph, to desribe the relations, and this graph shouldn’t have cycles. So we need the so called directed acyclic graph (DAG).

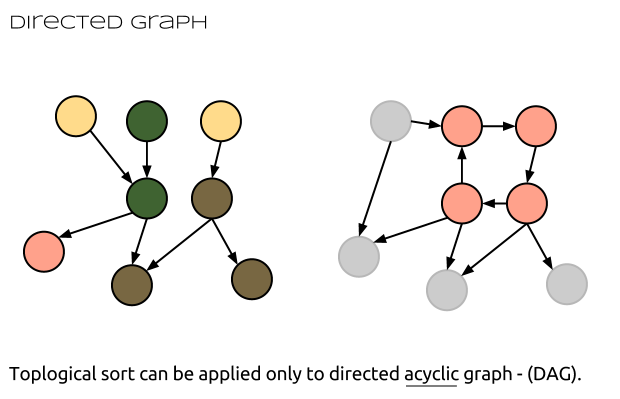
Why we don’t what a cycle in the graph? The answer of this question is simple and obvious. In case of cyclic graph, we wouldn’t be able to determine the priority of task execution, thus we won’t be able to sort the tasks properly.

Now the solution we want is to sort the vertices of the graph in some order so for each edge (u, v) u will precede v. Then we’ll have a linear order of all tasks and by starting their execution we’ll know that everything will be OK.

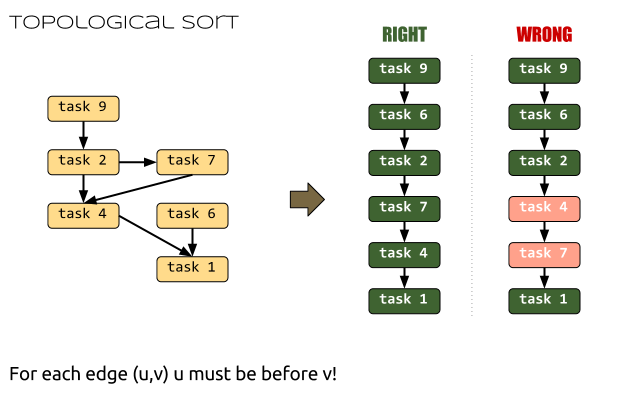
This kind of sort is also known as “topological” sort (or topsort) and it is one of the very basic graph algorithms. Continue reading Computer Algorithms: Topological Sort of a Graph →