Introduction

Linked lists are one very common and handy data structure that can be used in many cases of the practical programming. In this post we’ll assume that we’re talking about singly linked list. This means that each item is pointed by it’s previous item and it points to it’s next item. In this scenario the first item of the list, its head, doesn’t have an ancestor and the last item doesn’t have a successor.

Sometimes, due to bugs or bad architecture or complexity of the applications we can have problems with lists. One very typical problem is having a loop, which in breve means that some of the items of the list is pointed twice, as shown on the image below.

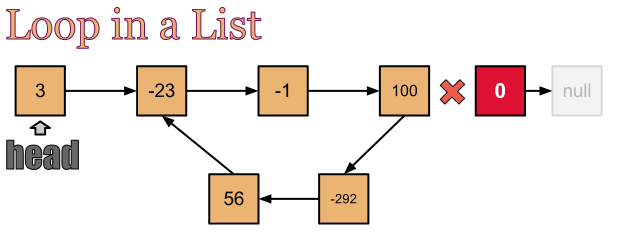
So in first place we need to be sure that there is a loop and then: how can we break it!

There are several algorithms on finding a loop, but here’s one very basic. It’s known as the Floyd’s algorithm or the algorithm of the tortoise and hare.

Overview

The Floyd’s algorithm relies on one very simple idea. Initially we set two pointers to the head of the list.

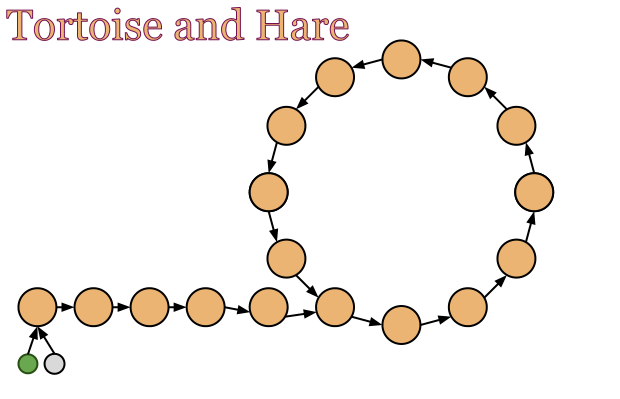
On each step we increment both pointers, but the hare is incremented by two elements, while the tortoise walks on every single item – as shown on the images bellow.

The tortoise, as it’s clear from the image bellow, is much slower.

As a result if we don’t have a loop in the list the hare will hit the end of the list, but if we do have a loop the hare will catch-up the tortoise inside the loop.

Code

Assuming a typical representation of a singly linked list here’s a sample code in PHP.

The Item Class

class Item
{
    protected $_name = '';
    protected $_key = '';
    protected $_next = null;
 
    public function __construct($key, $name)
    {
        $this->_key = $key;
        $this->_name = $name;
    }
 
    public function setNext(&$next) { $this->_next = $next; }
    public function &getNext() { return $this->_next; }
 
    public function setKey($key) { $this->_key = $key; }
    public function getKey() { return $this->_key; }
 
    public function setName($name) { $this->_name = $name; }
    public function getName() { return $this->_name; }
 
    public function __toString()
    {
        return $this->_key . ' ' . $this->_name . "\n";
    }
}

The List Class

class Linked_List 
{
    protected $_head = null;
 
    public function insert($item)
    {
        if ($this->_head == null) {
            $this->_head = $item;
            return;
        }
 
        $current = $this->_head;
        while ($current->getNext()) {
            $current = $current->getNext();
        }
 
        $current->setNext($item);
    }
 
    public function detectLoop()
    {
        $tortoise = $hare = $this->_head;
 
        if ($hare->getNext() != null) {
            $hare = $hare->getNext()->getNext();
        } else {
            return FALSE;
        }
 
        while ($hare) {
            if ($hare == $tortoise) {
                return $hare;
            }
 
            if ($hare->getNext()) {
                $hare = $hare->getNext()->getNext();
            } else {
                return FALSE;
            }
 
            $tortoise = $tortoise->getNext();
        }
 
        return FALSE;
    }
 
    protected function _isReachable($a, $b) 
    {
        $current = $b;
        while ($current->getNext() != $b) {
            if ($current->getNext() == $a) {
                return $current;
            }
            $current = $current->getNext();
        }
 
        return FALSE;
    }
 
    public function breakLoop()
    {
        if (FALSE === ($loop = $this->detectLoop())) {
            return;
        }
 
        $startOfTheLoop = $this->_head;
 
        while (FALSE === ($lastLoopItem = $this->_isReachable($startOfTheLoop, $loop))) {
            $startOfTheLoop = $startOfTheLoop->getNext();
        }
 
        $pseudoNext = null;
        $lastLoopItem->setNext($pseudoNext);
    }
 
    public function __toString()
    {
        $current = $this->_head;
        $output = '';
 
        while ($current) {
            $output .= $current->getKey() . ' ' . $current->getName() . "\n";
            $current = $current->getNext();
        }
 
        return $output;
    }
}

Initialization

$items = array(); $ll = new Linked_List();   for ($i = 0; $i < 100; $i++) { $items[$i] = new Item($i, 'Item #' . $i); $ll->insert($items[$i]); }   // 0 Item #0 // 1 Item #1 // ... // 99 Item #99 echo $ll;

$items = array(); $ll = new Linked_List(); for ($i = 0; $i < 100; $i++) { $items[$i] = new Item($i, 'Item #' . $i); $ll->insert($items[$i]); } // 0 Item #0 // 1 Item #1 // ... // 99 Item #99 echo $ll;

Breaking the Loop

In order to break the loop we need first to check whether an item is reachable from within the loop. Once we know that we should return the last loop item in order to improve the performance of the next method – breakLoop. This is made with the following method:

    protected function _isReachable($a, $b) 
    {
        $current = $b;
        while ($current->getNext() != $b) {
            if ($current->getNext() == $a) {
                return $current;
            }
            $current = $current->getNext();
        }
 
        return FALSE;
    }

Now we can break the loop by removing the double link to the first item of the loop.

    // member of Linked_List
    public function breakLoop()
    {
        if (FALSE === ($loop = $this->detectLoop())) {
            return;
        }
 
        $startOfTheLoop = $this->_head;
 
        while (FALSE === ($lastLoopItem = $this->_isReachable($startOfTheLoop, $loop))) {
            $startOfTheLoop = $startOfTheLoop->getNext();
        }
 
        $pseudoNext = null;
        $lastLoopItem->setNext($pseudoNext);
    }

Complexity

Assuming that the list length is N and the loop length is M, we’ll break the loop in O((N-M)*M) time complexity only after we’ve found the loop. The question is how fast we can find the loop with the algorithm above? Well the hare is pretty fast and can pass through some of the items of the loop several times, but the tortoise walks sequentially over all the items. The question is will the hare catch-up the tortoise before the last one gets to the end of the loop? The answer is yes and we can think of a single linked list without loops where there are two pointers starting from the beginning of the list. The same question can be translated to: will the faster pointer reach the end before the slower one gets to the middle of the list – well yes.

Finally the answer is O(N) for answering whether there’s a loop and O(M*(N-M)) to break it.

However the good news is that when we work with linked lists we often work only with pointers (which is our case in this post) and thus we don’t need additional memory which makes them very useful. Actually we will see the same advantage in the next algorithm – reversing a linked list, which is more effective than reversing an array.