If algorithms on stoimen.com were metro stations – here’s a map!

Please click on the image for a larger image!
1. Which is the fastest searching algorithm?
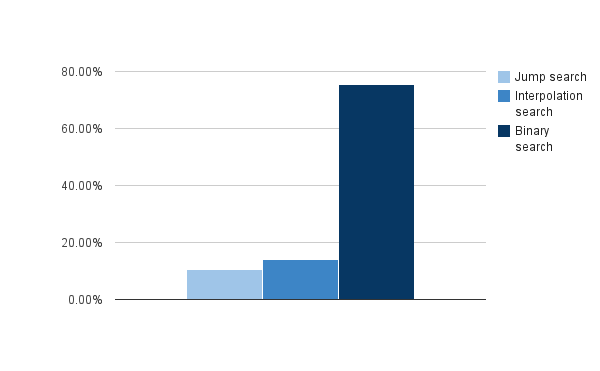
Continue reading You think you know algorithms. Quiz results!
As we all know most of the cases a program execution time depends most from the input data. As I wrote in my post the degree of the input data estimates the algorithm complexity.
Of course 3*n² is a bit faster than 5*n², but in general both functions are similar and have the same complexity. In this case we tend to say that the size of the input data is n.

It is easy to bind this to arrays or other simple data structures. For example when sorting an array with n elements, the size of the input data is n, but sometimes there is not such an obvious relation between an algorithm and the size of the input data.
For instance when we’ve to search a path into a graph, than maybe the best way to describe the input data is by summing both the number of vertices and the number of edges.

However this is important when dealing with algorithms, because a mistake in the estimation of the input data size will result in wrong algorithm estimation at all

When a programmer sees a chunk of code he tends to evaluate it in a rather intuitive manner and to qualify it as “elegant” or not. This is quite easy, because it’s subjective and nobody knows what exactly elegant means. However behind this there is a powerful mathematical approach of measuring a program effectiveness.
It’s a pity that most of the developers still think of the big O notation as something from the university classes, but unusual in the practice and they barely use it their job. But before describing the big O notation, let me start from something really simple.
Let’s have the following example (note that all the examples are in PHP):
$n = 100; $s = 0; for ($i = 0; $i < $n; $i++) { for ($j = 0; $j < $n; $j++) { $s++; } } |
As you can see there are two assignments and two nested loops. This is really a widely used example from any algorithm book.
First of all the time to assign a value to a variable, to compare two values and to increment a variable is constant. It depends on the computer resources, the compiler or the language, but it’s constant on one machine if you compare two chunks of code. Now we can see that these operations take (add) constant time to the program, and we can assume this time is respectively a, b, c, d, e, f, g, h, i.
$n = 100; // a $s = 0; // b $i = 0; // c $i < $n; // d $i++; // e $j = 0; // f $j < $n; // g $j++; // h $s++; // i |
Actually the most important thing here is the value of n. By assigning greater values to n the more time will take the program to run. As we can see from the following table by multiplying the value of n by 10, the time became 100 times more.
n time 10 0.00002 100 0.002 ... ... |
What happens in fact is that we can sum all these values.
a + b + c + n*d + n*e + n*(f + n*g + n*h + n*i) |
and by substituting:
a + b + c = k d + e + n = l g + h + i = m |
the result is:
m*n² + l*n + k |
Here the most important thing is the degree of n, because it can change dramatically the program time consumption depending on the n value. Thus this chunk has a quadratic complexity or O(n²).
Of course there are constants, but in the practice they are not so important. Take a look at these two functions:
f = 2*n² g = 200*n |
OK, for n = 1 the first one will be faster, but as n increments the second function becomes to be faster and faster, thus after a given value of n the second function is really the fastest!